サイコロの目の和の問題
　　　ｒ個の面があるｎ個のサイコロを投げて、それぞれのサイコロの目の和がｋとなる場合の数は？

解答.
　ｒ＝6、n＝5、k=8、下図のように4つの仕切りと8個の丸によって起こり得る状態を表す事ができます。
　　　　　　

　　左から1番目の仕切りより左にある丸は、1つめのサイコロの目を左から1番目の仕切りから2番目の仕切りの間にある丸が2つめのサイコロの目を表しています。
　同様に、仕切り2,3の間が3つめのサイコロのを、仕切り3,4の間が4つめのサイコロの目を、そして仕切り4より右が5つ目のサイコロの目を表します。
　この状態の数は組み合わせ論の計算によって次のようになります。
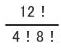　しかしこれでは、仕切りの区間内に丸が全く無い場合まで含まれています。各区間に少なくとも1つの丸があるわけですから8-5＝3で3個の丸がどの区間
にあるのか分かればよいのです。この場合の数はとなります。
これで仕切りの区間に丸が少なくとも1つある場合の数を場合を数え上げました。
今度は、　ｒ＝6、n＝2、k=10、の場合を考えます。
　下図は、仕切りの左右に少なくとも1つの丸がある場合を調べるために、10-2＝8で8個の丸があります。
　　
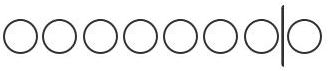
　しかしこの場合には、仕切りよりも左側に7個の丸があり、　ｒ＝6、条件を満たしません。
1つの仕切りの区間に6個以上の丸があるとこのように条件を満たしません。仕切りより左側に少なくとも6個の丸が存在する場合の数は、8-6＝2で2個の丸が仕切りのどちら側にあるかを調べれば分かります。この場合の数は3通りです。
同様に仕切りの右側に少なくとも6個の丸が存在する場合の数は、3通りとなります。
したがって、求めるべき場合の数は、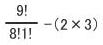となります。
次に、ｒ＝6、n＝2、k=14　という条件で考えてみます。すると下図の様に仕切りの両側に6個の丸が存在する場合があります。

したがって、求めるべき場合の数は、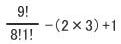
一般的な式を得るためには、左から1番目の仕切りの左に6個以上の丸がある場合をA1,左からi-1番目とi番目の仕切りの間の6個以上の丸がある場合をAi、左から数えて最後の仕切り（左ｎ-1番目）の右に6個以上の丸がある場合をAn-1として、
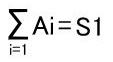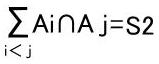　,,,等として、包除原理の式
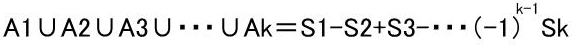　を使って次の様になります。
　　　　　　　　　　　　　　　　　　　
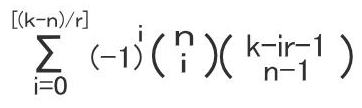
[　　]内の数字はｋ-ｎをｒで割った値から小数点以下を切り捨てた値です。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　トップページへ